猩猩的乐园

原题说明

In a binary tree, the root node is at depth 0, and children of each depth k node are at depth k+1.

Two nodes of a binary tree are cousins if they have the same depth, but have different parents.

We are given the root of a binary tree with unique values, and the values x and y of two different nodes in the tree.

Return true if and only if the nodes corresponding to the values x and y are cousins.

Example 1: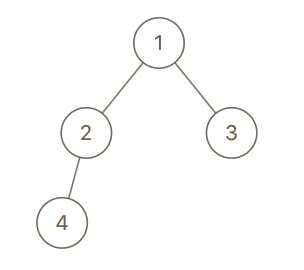

Input: root = [1,2,3,4], x = 4, y = 3
Output: false

Example 2: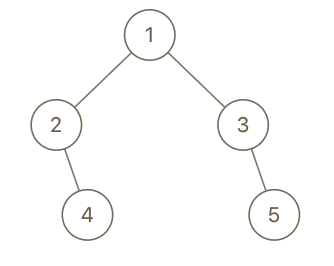

Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true

Example 3: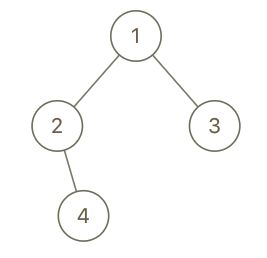

Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false

Note:

1. The number of nodes in the tree will be between 2 and 100.
2. Each node has a unique integer value from 1 to 100.
   Read more »

原题说明

In a given grid, each cell can have one of three values:

• the value 0 representing an empty cell;
• the value 1 representing a fresh orange;
• the value 2 representing a rotten orange.

Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1 instead.

Example 1:

Input: [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Note:

1. 1 <= grid.length <= 10
2. 1 <= grid[0].length <= 10
3. grid[i][j] is only 0, 1, or 2.
   Read more »

原题说明

Write a function to find the longest common prefix string amongst an array of strings.

If there is no common prefix, return an empty string "".

Example 1:

Input: [“flower”,”flow”,”flight”]
Output: “fl”

Example 2:

Input: [“dog”,”racecar”,”car”]
Output: “”

Note:

All given inputs are in lowercase letters a-z.

解题思路

本题解法大致分为两步. 第一步获取输入中字符串的最小长度, 用来防止之后访问时的内存越界. 第二步, 依次判断字符串第i位的字符是否一样.
需要特别注意一些边界条件, 如输入空列表时直接返回空字符创.

示例代码 (python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Solution(object):
    def reverse(self, x):
        """
        :type x: int
        :rtype: int
        """
        if len(strs) == 0:
            return ''
        ret = ''
        min_len = len(strs[0])
        for i in range(1, len(strs)):
            if len(strs[i]) < min_len:
                min_len = len(strs[i])
        
        for i in range(min_len):
            for j in range(1, len(strs)):
                if strs[j][i] != strs[0][i]:
                    return ret
            ret += strs[0][i]
        return ret

复杂度分析

时间复杂度: O(NK). N为列表长度, K为字符串长度
空间复杂度: O(K). K为字符串长度

归纳总结

本题比较简单, 但是仍需注意边界条件, 不要大意出错.

原题说明

Determine whether an integer is a palindrome. An integer is a palindrome when it reads the same backward as forward.

Example 1:

Input: 121
Output: true

Example 2:

Input: -121
Output: false
Explanation: From left to right, it reads -121. From right to left, it becomes 121-. Therefore it is not a palindrome.

Example 3:

Input: 10
Output: false
Explanation: Reads 01 from right to left. Therefore it is not a palindrome.

解题思路

最简单的思路是先转换成字符串, 然后用两个指针来判断. 但是这样需要O(n)的空间复杂度. 为了用O(1)的空间复杂度, 我们可以直接把输入转换成反转后的数字. 如果一个数字反转后, 大小不变, 则是回文数. 解法也比较直观, 按位取余后逐渐生成反转后的数字. 要注意判断是否溢出.

示例代码 (python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution(object):
    def isPalindrome(self, x):
        """
        :type x: int
        :rtype: bool
        """
        if x < 0:
            return False
        rev = 0
        x_ = x
        while x_ > 0:
            tmp = rev * 10 + x_ % 10
            if (tmp - x_ % 10 ) / 10 != rev:
                return False
            rev = tmp
            x_ /= 10
        return x == rev

复杂度分析

时间复杂度: O(n)
空间复杂度: O(1)

归纳总结

在解题时需要判断是否会溢出.

原题说明

Given a 32-bit signed integer, reverse digits of an integer.

Example 1:

Input: 123
Output: 321

Example 2:

Input: -123
Output: -321

Example 3:

Input: 120
Output: 21

Note:

Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−2^31, 2^31 − 1].
For the purpose of this problem, assume that your function returns 0 when the reversed integer overflows.

解题思路

解法比较简单, 按位取余即可. 难点在于如何处理溢出的问题. 在python中, 会自动处理溢出问题, 只需要直接判断是否在INT_32的范围内即可.
但是python的取余在负数上的行为与预期不同, 因此需要记下符号, 并转换成非负数. 其他语言中, 需要在结果乘10之前与INT_MAX作比较，观察是否会溢出.

示例代码 (python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution(object):
    def reverse(self, x):
        """
        :type x: int
        :rtype: int
        """
        sign = 1 if x > 0 else -1
        x = x if x > 0 else -x
        ret = 0
        while x != 0:
            ret *= 10
            ret += x % 10
            x /= 10
        ret *= sign
        if (ret < -2**31) or (ret > 2**31 - 1):
            return 0
        return ret

复杂度分析

时间复杂度: O(log n)
空间复杂度: O(1)

归纳总结

在解题时需要考虑清楚何时会溢出, 或者转换成长整型后再作判断.

原题说明

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.

If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).

The replacement must be in-place and use only constant extra memory.

Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.

1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

解题思路

不熟悉排列数的，可以看一下permutation的基本定义。同时，我们要清楚字典顺序的定义Lexicographical order。

最直接的想法是把所有的全排列找出，但是这显然不是最优解，并且不符合题目要求的constant extra memory。

我们这里用一个例子来说明如何找出下一个字典顺序的排列数。
假定我们有下面这组排列是

6 5 4 8 7 5 1

• 我们从后往前看，找到第一个非递减的数，这里是 4 .
• 我们可以发现，以 6 5 4开头的排列数，8 7 5 1 已经是最后一个排列数，因此需要把 4 做替换
• 在 8 7 5 1 中，比 4 大的最小的数是 5，因此把 5 和 4 做交换，我们得到 6 5 5 8 7 4 1
• 显然 6 5 5 8 7 4 1 并不是我们要求的，但只要把最后 4 位 8 7 4 1 做从小到大的排序，变成 1 4 7 8, 我们就得到了想要的字典顺序的排列数 6 5 5 1 4 7 8。

按照这个思路，我们给出相对应的代码。

示例代码 (cpp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int n = nums.size(), left = -1;
        for (int i = n-1; i > 0; i--) {
            if (nums[i-1] < nums[i]) {
                left = i-1;
                break;
            }
        }
        if (left != -1) {
            for (int i = n-1; i > left; i--) {
                if (nums[left] < nums[i]) {
                    swap(nums[left], nums[i]);
                    break;
                }
            }
        }
        reverse(nums.begin() + left + 1, nums.end());
    }
};

复杂度分析

搜索第一个非递减的数，复杂度为 O(n)，reverse数组，复杂度为 O(n), 所以总的时间复杂度是 O(n) 。
没用额外空间，复杂度是 O(1)。

• 时间复杂度: O(n)
• 空间复杂度: O(1)

归纳总结

这题主要需要先明白 permutation 和 lexicographical order, 然后才能找出 next permutation的规律。借助一些具体的例子，能帮助提供一些思路。比单纯抽象的思考可能更好。

原题说明

The string "PAYPALISHIRING" is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)

1
2
3

P   A   H   N
A P L S I I G  
Y   I   R

And then read line by line: "PAHNAPLSIIGYIR"

Write the code that will take a string and make this conversion given a number of rows:

string convert(string s, int numRows);

Example 1:

1
2

Input: s = "PAYPALISHIRING", numRows = 3
Output: "PAHNAPLSIIGYIR"

Example 2:

1
2
3
4
5
6
7

Input: s = "PAYPALISHIRING", numRows = 4
Output: "PINALSIGYAHRPI"
Explanation:
P     I    N
A   L S  I G
Y A   H R
P     I

解题思路

这道题需要把一个字符串变成ZigZag的排列后按行输出。所以我们只需要依次判断每个字符应该出现在ZigZag排列中的哪一行就可以了。
对于一个N行的ZigZag排列，我们可以把它看作一个周期为2N - 2的循环。在这个周期内，如果一个字符位于周期的前N位，
那么它的位数就是行号。如果在N位置后，那么它的行号就是超出部分的倒序，如N + 1那么，行号就是N - 1. (以上行号，从1开始计)

示例代码 (python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution(object):
    def convert(self, s, numRows):
        """
        :type s: str
        :type numRows: int
        :rtype: str
        """
        if numRows == 1:
            return s
        rows = ['' for i in range(numRows)]
        for i in range(len(s)):
            r = i % (2 * numRows - 2)
            if r >= numRows:
                r = 2 * numRows - r - 2
            rows[r] += s[i]
        return ''.join(rows)

复杂度分析

时间复杂度: O(n) 其中n为s的长度
空间复杂度: O(n)

归纳总结

这道题难度不高, 只需要考虑清楚字符串转换前后的对应关系即可。

原题说明

Determine if a 9x9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:

1. Each row must contain the digits 1-9 without repetition.
2. Each column must contain the digits 1-9 without repetition.
3. Each of the 9 3x3 sub-boxes of the grid must contain the digits 1-9 without repetition.

The Sudoku board could be partially filled, where empty cells are filled with the character '.'.

Example 1:

Input:
[
[“5” , “3” , “ . “ , “ . “ , “7” , “ . “ , “ . “ , “ . “ , “ . “],
[“6” , “ . “ , “ . “ , “1” , “9” , “5” , “ . “ , “ . “ , “ . “],
[“ . “ , “9” , “8” , “ . “ , “ . “ , “ . “ , “ . “ , “6” , “ . “],
[“8” , “ . “ , “ . “ , “ . “ , “6” , “ . “ , “ . “ , “ . “ , “3”],
[“4” , “ . “ , “ . “ , “8” , “ . “ , “3” , “ . “ , “ . “ , “1”],
[“7” , “ . “ , “ . “ , “ . “ , “2” , “ . “ , “ . “ , “ . “ , “6”],
[“ . “ , “6” , “ . “ , “ . “ , “ . “ , “ . “ , “2” , “8” , “ . “],
[“ . “ , “ . “ , “ . “ , “4” , “1” , “9” , “ . “ , “ . “ , “5”],
[“ . “ , “ . “ , “ . “ , “ . “ , “8” , “ . “ , “ . “ , “7” , “9”]
]
Output: true

Example 2:

Input:
[
[“8” , “3” , “ . “ , “ . “ , “7” , “ . “ , “ . “ , “ . “ , “ . “],
[“6” , “ . “ , “ . “ , “1” , “9” , “5” , “ . “ , “ . “ , “ . “],
[“ . “ , “9” , “8” , “ . “ , “ . “ , “ . “ , “ . “ , “6” , “ . “],
[“8” , “ . “ , “ . “ , “ . “ , “6” , “ . “ , “ . “ , “ . “ , “3”],
[“4” , “ . “ , “ . “ , “8” , “ . “ , “3” , “ . “ , “ . “ , “1”],
[“7” , “6” , “ . “ , “ . “ , “ . “ , “ . “ , “2” , “8” , “ . “],
[“ . “ , “ . “ , “ . “ , “4” , “1” , “9” , “ . “ , “ . “ , “5”],
[“ . “ , “ . “ , “ . “ , “ . “ , “8” , “ . “ , “ . “ , “7” , “9”]
]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being modified to 8. Since there are two 8’s in the top left 3x3 sub-box, it is invalid.

Note:

• A Sudoku board (partially filled) could be valid but is not necessarily solvable.
• Only the filled cells need to be validated according to the mentioned rules.
• The given board contain only digits 1-9 and the character ‘.’.
• The given board size is always 9x9.

解题思路

本题要求确定一个 9 x 9 的数独是否valid。题目说明并不要求数独是可解的，因此难度不是很高。

根据数独的规则，需要对每一行，每一列，以及规定的 9 个 3 x 3 的矩阵做检查。因为每次检查需要对9个数进行查重，我们另外写一个函数 isValidSec ，用一个map记录下遍历过的值，遇到有相同的数字是返回false, 否则最终返回true。
然后分别按行、列、矩阵块遍历即可。

具体代码如下：

示例代码 (cpp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        vector<char> nineNum;
        // 检查行
        for (int i = 0; i < board.size(); i++) {
            if (!isValidSec(board[i])) {
                return false;
            }
        }
        // 检查列
        for (int i = 0; i < board[0].size(); i++) {
            nineNum.clear();
            for (int j = 0; j < board.size(); j++) {
                nineNum.push_back(board[j][i]);
            }
            if (!isValidSec(nineNum)) {
                return false;
            }
        }
        // 检查矩阵块
        for (int i = 0; i < board.size(); i = i + 3) {
            for (int j = 0; j < board[0].size(); j = j + 3) {
                nineNum.clear();
                for (int l = i; l < i+3; l++){
                    for (int m = j; m < j+3; m++){
                        nineNum.push_back(board[l][m]);
                    }
                }
                if (!isValidSec(nineNum)) {
                    return false;
                }
            }
        }
        return true;
    }
    bool isValidSec(vector<char>& nineNum) {
        unordered_map<char, int> table;
        for(int i = 0 ; i < nineNum.size(); i++) {
            if (nineNum[i] != '.' && table.count(nineNum[i]) > 0) {
                return false;
            }
            else {
                table[nineNum[i]] = 1;
            }
        }
        return true;
    }
};

复杂度分析

我们遍历了3遍整个数独，因此时间复杂度为O(n), 同时空间复杂度为O(n^0.5).

• 时间复杂度: O(n)
• 空间复杂度: O(n^0.5)

归纳总结

这题的难度不高，按照数独的规则一次做检查即可。代码虽然显得较长，但可读性会显得比较好。之后我们会再介绍这题的进阶版，[LeetCode 37] Sudoku Solver。

原题说明

Given an input string (s) and a pattern (p), implement regular expression matching with support for '.' and '*'.

‘.’ Matches any single character.
‘*’ Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

Note:

• s could be empty and contains only lowercase letters a-z.
• p could be empty and contains only lowercase letters a-z, and characters like . or *.

Example 1:

Input:
s = “aa”
p = “a”
Output: false
Explanation: “a” does not match the entire string “aa”.

Example 2:

Input:
s = “aa”
p = “a*“
Output: true
Explanation: ‘*‘ means zero or more of the precedeng element, ‘a’. Therefore, by repeating ‘a’ once, it becomes “aa”.

Example 3:

Input:
s = “ab”
p = “.*“
Output: true
Explanation: “.*“ means “zero or more (*) of any character (.)”.

Example 4:

Input:
s = “aab”
p = “c*a*b”
Output: true
Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore it matches “aab”.

Example 5:

Input:
s = “mississippi”
p = “mis*is*p*.”
Output: false

解题思路

以下解题思路以python版本为准, cpp版本则是简化的(无递归)动态规划解答, 读者任选其一即可

如果熟悉Edit distance的话, 可以比较容易得想到用动态规划的办法求解.
类似Edit distance的解法, 我们可以构建一个SxP的矩阵来记录状态.
该矩阵中位于坐标i, j的值代表字符串s[i:]和Patternp[j:]是否匹配(若为None, 则代表未知).
求解该矩阵的过程可以看作遵循一定走法的同时，试图寻找一条从(0, 0)走到(S + 1, P + 1)的路径. (S + 1和P + 1可以看作是s和p的终结状态)

如果s[i]和p[j]是匹配的(s[i] == p[j] 或者 p[j] == '.'):

• 如果j + 1是*的话，我们可以从(i, j)走到(i, j + 2)代表我们跳过这个pattern, 或者从(i, j)走到(i + 1, j)代表我们选择匹配这个字符
• 如果不是*的话，那么我们直接从(i, j)走到(i + 1, j + 1). 这意味着我们匹配了(i, j)

如果不匹配:

• 如果j + 1是*的话, 我们可以从(i, j)走到(i, j + 2)代表我们跳过这个pattern
• 如果不是, 那么说明必然不匹配, (i, j)的状态是False
  终结状态就是s和p都用完, 也就是走到(S + 1, P + 1)的时候.
  如果p用完了, 但是s还有剩余, 那么显然不匹配.
  如果s用完了, p还有剩余, 那么只有当接下来都是有*的pattern的时候才匹配.

示例代码 (python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution(object):
    def dfs(self, i, j, s, p, dp):
        if j == len(p):
            return i == len(s)
        
        if i == len(s):
            if j < len(p) - 1 and p[j + 1] == '*':
                return self.dfs(i, j + 2, s, p, dp)
            else:
                return False
            
        if dp[i][j] is not None:
            return dp[i][j]
        
        curr_match = p[j] == '.' or s[i] == p[j]
        if j + 1 < len(p) and p[j + 1] == '*':
            dp[i][j] = self.dfs(i, j + 2, s, p, dp) \
                        or curr_match and self.dfs(i + 1, j, s, p, dp)
        else:
            dp[i][j] = curr_match and self.dfs(i + 1, j + 1, s, p, dp)
        return dp[i][j]
    def isMatch(self, s, p):
        """
        :type s: str
        :type p: str
        :rtype: bool
        """
        dp = [[None for i in range(len(p))] for j in range(len(s))]
        return self.dfs(0, 0, s, p, dp)

示例代码 (cpp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size(), n = p.size();
        vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, false));
        dp[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (p[j - 1] != '*' && p[j - 1] != '.') {
                    if (i > 0 && s[i - 1] == p[j - 1]) {
                        dp[i][j] = dp[i - 1][j - 1];
                    }
                } else if (p[j - 1] == '.') {
                    if (i > 0) {
                        dp[i][j] = dp[i - 1][j - 1];
                    }
                } else {
                    if (j == 1) {
                        continue;
                    }
                    dp[i][j] = dp[i][j - 2];
                    if (i > 0 && (p[j - 2] == '.' || p[j - 2] == s[i - 1])) {
                        dp[i][j] = dp[i][j] || dp[i - 1][j];
                    }
                }
            }
        }
        return dp[m][n];
    }
};

复杂度分析

时间复杂度: O(SP), 其中S为s的长度, P为p的长度.
空间复杂度: O(SP), 其中S为s的长度, P为p的长度

归纳总结

这道题的思路还是比较容易想到用动态规划/递归来做的. 虽然这里python版本使用了DFS，但是因为记录了中间状态，本质上就是动态规划(如果读者细心比较，会发现时间空间复杂度也是一样的). 面试时, 还需要额外注意终结状态的判断和边界条件, 避免出现edge case或者访问了超出边界的矩阵坐标.

原题说明

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Input: "cbbd"
Output: "bb"

解题思路

很多palindrome相关的问题都可以用动态规划去解决. 做动态规划的问题, 要想清楚以下几件事情:

• 动归数组代表了什么
• 递推公式是什么, 从而可以决定从什么方向开始递推. 例如dp[i] = func(dp[i-1])那就从左向右递推, 反之如果dp[i] = func(dp[i+1])那么就要从右向左递推
• 处理边界条件

回到这道题, 我们用一个二维布尔数组dp[j][i]代表从j开始到i结束的子字符串是否为回文字符串. 初始条件为对于任意下标i, dp[i][i]为true, 这一初始条件可以在递推过程中更新. 递推公式和递推方向请见具体代码.

示例代码 (cpp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    string longestPalindrome(string s) {
        if (!s.size()) {
            return "";
        }
        string ret;
        int left = 0, maxLen = 1;
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n, false));
        for (int i = 0; i < n; ++i) { // i自左向右更新
            dp[i][i] = true;
            for (int j = i - 1; j >= 0; --j) { // j自右向左更新
                dp[j][i] = (s[i] == s[j] && (i - j < 2 || dp[j + 1][i - 1]));
                // 上面这行就是递推公式
                if (dp[j][i]) {
                    if (maxLen < i - j + 1) {
                        maxLen = i - j + 1;
                        left = j;
                    }
                }
            }
        }
        return s.substr(left, maxLen);
    }
};

示例代码 (python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        maxlen = 0
        ret = None
        dp = [[None for i in range(len(s))] for j in range(len(s))]
        for right in range(len(s)):
            for left in range(right, -1, -1):
                dp[left][right] = s[left] == s[right] and (right - left < 3 or dp[left + 1][right - 1])
                if dp[left][right] and (right - left + 1 > maxlen):
                    maxlen = right - left + 1
                    ret = s[left:right + 1]
        return ret

复杂度分析

时间复杂度: O(n^2), 其中n为s的长度
空间复杂度: O(n^2)

归纳总结

动态规划的题一般思路比较难想清楚, 但是有了思路之后代码实现比较容易. 因此面试中不要慌张, 记住本文归纳的三个要点, 先讨论清楚了再开始写代码.