[Leetcode 802] Find Eventual Safe States

原题说明

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph. If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node. More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe? Return them as an array in sorted order.

The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph. The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
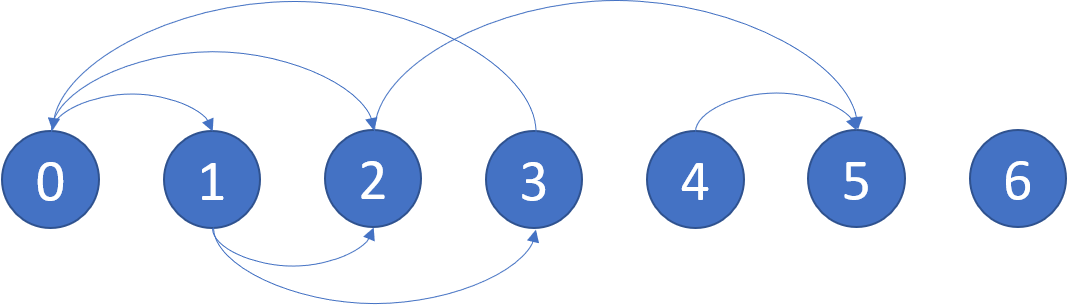
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]

Note:

graph will have length at most 10000.
The number of edges in the graph will not exceed 32000.
Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

解题思路

首先需要理解题意, 所谓safe node是指所有经过该node的路径都最后结束于terminal node, 也就是说不会形成环.
所以我们可以给每个node三个状态,分别为:

0: unvisited
1: unsafe
2: safe

利用dfs遍历每一个node (返回值为当前路径是否safe):

如果node的状态为unvisited, 那么我们初始化该node转态为unsafe, 并用dfs遍历其所有路径,如果其中有任意一条范围为unsafe, 那么直接break. 如果所有路径返回均为safe,那么设该node状态为safe并返回.
如果node状态为unsafe, 那么有两种情况, 要么是之前dfs遍历时访问过, 确定为unsafe状态; 要么是当前访问路径下之前经过了该点, 说明当前路径形成了环. 不管是哪一种情况, 当前node的unsafe状态都不会改变, 直接返回false.
如果node状态为safe, 那么肯定是之前dfs遍历过, 确定为safe状态, 直接返回即可.

示例代码 (cpp)

class Solution {
    bool dfs(vector<vector<int>>& graph, vector<int>& states, int cur) {
        if (states[cur] == 1) {
            return false;
        }
        if (states[cur] == 2) {
            return true;
        }
        states[cur] = 1;
        for (auto& nei : graph[cur]) {
            if (!dfs(graph, states, nei)) {
                return false;
            }
        }
        states[cur] = 2;
        return true;
    }
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
        vector<int> states(graph.size(), 0);
        for (int i = 0; i < graph.size(); ++i) {
            dfs(graph, states, i);
        }
        vector<int> rets;
        for (int i = 0; i < states.size(); ++i) {
            if (states[i] == 2) {
                rets.push_back(i);
            }
        }
        return rets;
    }
};

示例代码 (python)

class Solution(object):
    def dfs(self, graph, state, curr_idx):
        if state[curr_idx]:
            return state[curr_idx]
        state[curr_idx] = 1
        for next_node_idx in graph[curr_idx]:
            next_state = self.dfs(graph, state, next_node_idx)
            if next_state == 1:
                return state[curr_idx]
        state[curr_idx] = 2
        return state[curr_idx]
    
    def eventualSafeNodes(self, graph):
        """
        :type graph: List[List[int]]
        :rtype: List[int]
        """
        ret = []
        state = [0 for i in range(len(graph))]
        for idx in range(len(graph)):
            if self.dfs(graph, state, idx) == 2:
                ret.append(idx)
        return ret

复杂度分析

时间复杂度: O(n) 因为每个node经过一次
空间复杂度: O(n) 记录states

归纳总结

这是一道经典的DFS题目, 需要注意的是, 每个node有三个状态, 并且我们经过node时将其设为unsafe状态, 这样遍历过程中再次遇到该点, 我们就可以直接确定为unsafe了.