[Leetcode 1080] Insufficient Nodes in Root to Leaf Paths

原题说明

Given the root of a binary tree, consider all root to leaf paths: paths from the root to any leaf.  (A leaf is a node with no children.)

A node is insufficient if every such root to leaf path intersecting this node has sum strictly less than limit.

Delete all insufficient nodes simultaneously, and return the root of the resulting binary tree.

 

Example 1:

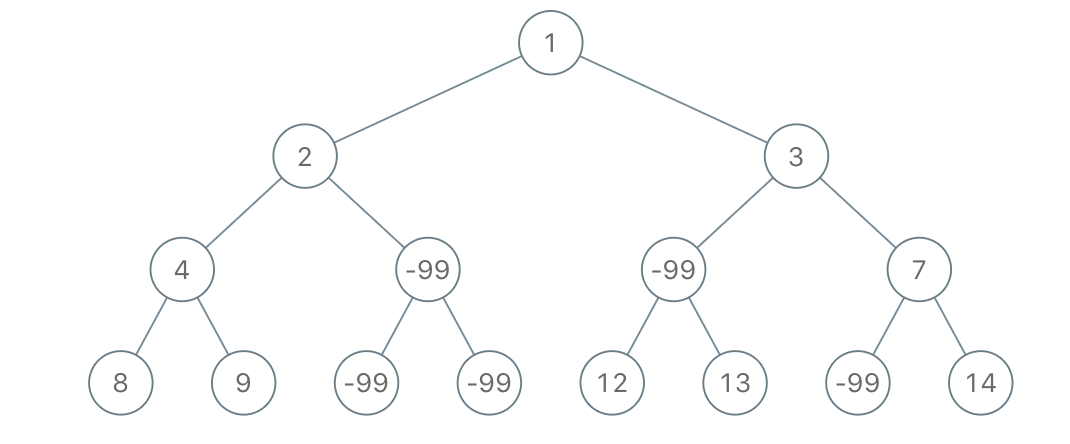
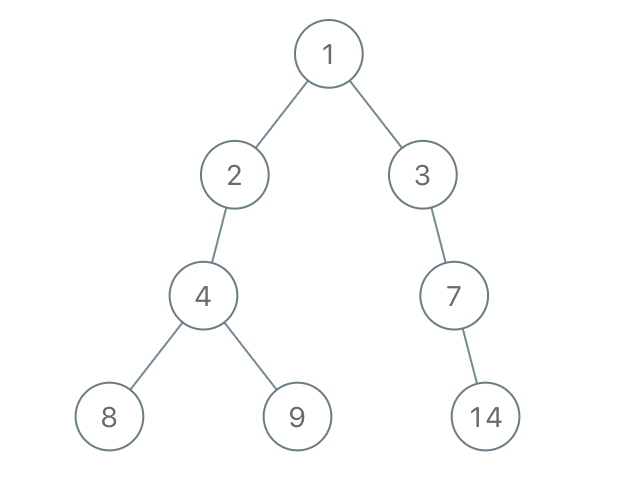
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1

Output: [1,2,3,4,null,null,7,8,9,null,14]

Example 2:

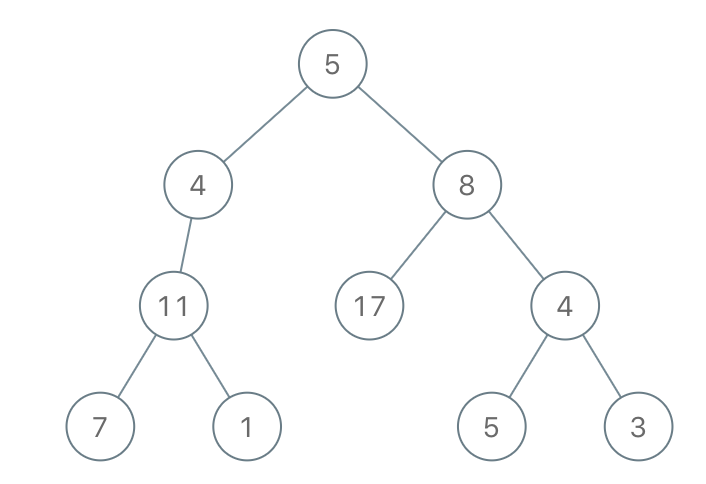
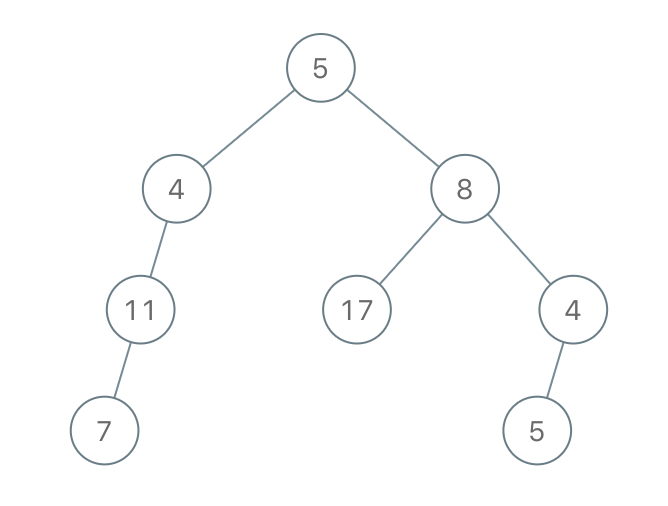
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22

Output: [5,4,8,11,null,17,4,7,null,null,null,5]

 

Example 3:

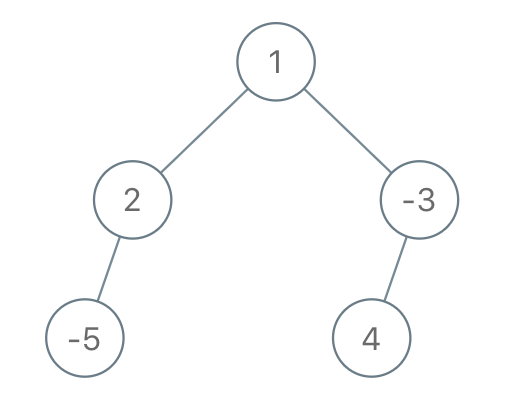
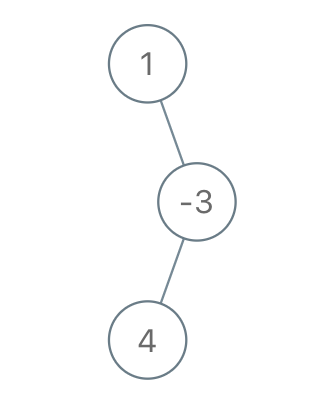
Input: root = [1,2,-3,-5,null,4,null], limit = -1

Output: [1,null,-3,4]

 

Note:

1. The given tree will have between 1 and 5000 nodes.
2. -10^5 <= node.val <= 10^5
3. -10^9 <= limit <= 10^9

解题思路

题目要去除所有不充分的点。这里对一个点是否充分的定义是：每一条从根节点开始，通过该点到达任意叶子节点的路径的和，都严格小于题目给出的值Limit。把所有不充分的点同时删除后，返回剩下的二叉树的根。
用dfs的方法解题，

1. 当一个节点是叶子节点时，直接判断它是否是充分的，如果不是，返回nullptr，否则返回该节点的指针。
2. 当一个节点不是叶子节点时，判断它的子节点是不是都是不充分的。如果都是不充分的，那么返回nullptr，也就是说它也是不充分的。否则返回该节点的指针。

工程上，C++可以选用smart pointer,从而不用考虑内存泄露的问题。

示例代码 (cpp)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        return helper(root, limit);
    }
    
private:
    TreeNode* helper(TreeNode* node, int limit, int cur = 0) {
        if (node == nullptr) {
            return nullptr;
        }
        cur += node->val;
        if (node->left == nullptr && node->right == nullptr) {
            if (cur < limit) {
                delete node;
                return nullptr;
            }
            return node;
        }
        node->left = helper(node->left, limit, cur);
        node->right = helper(node->right, limit, cur);
        if (node->left == nullptr && node->right == nullptr) {
            return nullptr;
        }
        return node;
    }
};

示例代码 (java)

class Solution {
    public TreeNode sufficientSubset(TreeNode root, int limit) {
        if (root == null)
            return null;
        if (root.left == null && root.right == null)
            return root.val < limit ? null : root;
        root.left = sufficientSubset(root.left, limit - root.val);
        root.right = sufficientSubset(root.right, limit - root.val);
        return root.left == root.right ? null : root;
    }
}

示例代码 (python)

class Solution(object):
    def sufficientSubset(self, root, limit):
        """
        :type root: TreeNode
        :type limit: int
        :rtype: TreeNode
        """
        if root.left == root.right:
            return None if root.val < limit else root
        if root.left:
            root.left = self.sufficientSubset(root.left, limit - root.val)
        if root.right:
            root.right = self.sufficientSubset(root.right, limit - root.val)
        return root if root.left or root.right else None

复杂度分析

时间复杂度: O(n)
空间复杂度: O(1)

视频讲解

我们在Youtube上更新了视频讲解，欢迎关注！