[Leetcode 1059] All Paths from Source Lead to Destination

原题说明

Given the edges of a directed graph, and two nodes source and destination of this graph, determine whether or not all paths starting from source eventually end at destination, that is:

• At least one path exists from the source node to the destination node
• If a path exists from the source node to a node with no outgoing edges, then that node is equal to destination.
• The number of possible paths from source to destination is a finite number.

Return true if and only if all roads from source lead to destination.

Example 1:

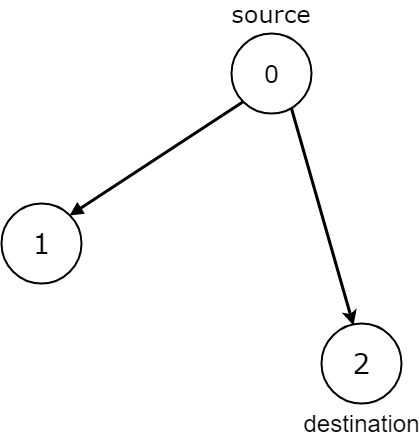
Input: n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
Output: false
Explanation: It is possible to reach and get stuck on both node 1 and node 2.

Example 2:

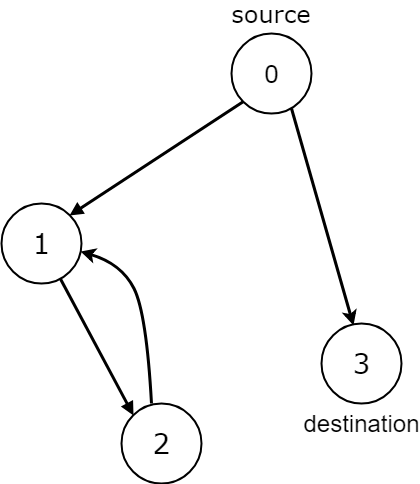
Input: n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
Output: false
Explanation: We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.

Example 3:

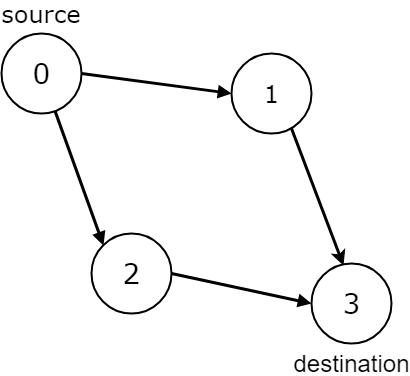
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
Output: true

Example 4:

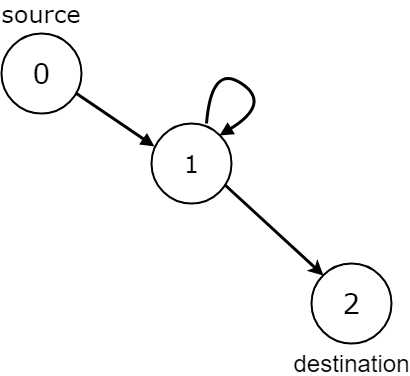
Input: n = 3, edges = [[0,1],[1,1],[1,2]], source = 0, destination = 2
Output: false
Explanation: All paths from the source node end at the destination node, but there are an infinite number of paths, such as 0-1-2, 0-1-1-2, 0-1-1-1-2, 0-1-1-1-1-2, and so on.

Example 5:

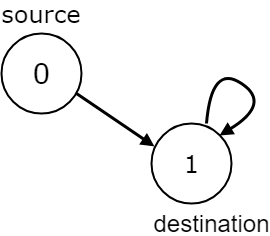
Input: n = 2, edges = [[0,1],[1,1]], source = 0, destination = 1
Output: false
Explanation: There is infinite self-loop at destination node.

Note:

1. The given graph may have self loops and parallel edges.
2. The number of nodes n in the graph is between 1 and 10000
3. The number of edges in the graph is between 0 and 10000
4. 0 <= edges.length <= 10000
5. edges[i].length == 2
6. 0 <= source <= n - 1
7. 0 <= destination <= n - 1

解题思路

使用DFS，用一个数组visited来记录以每一个节点为source，到destination应当返回的值(not visited, true, or false)。
然后要明确边界条件：

1. 当遇到一个没有出度的节点，则需要判断是否该点为destination，是的话返回true，不然则为false。
2. 判断当前节点是否被访问过，如果访问过，则返回visited对应的值。

在DFS中，要首先将visited[source]记录为isFalse, 然后再开始递归，这样遇到cycle，则会返回false，不然就会返回true，那就不对了。
DFS要求source的每一个child到destination都为true，这样source到destination也为true，反之则为false。

示例代码 (cpp)

class Solution {
    enum State {notVisited, isTrue, isFalse};
    bool dfs(const vector<vector<int>>& mapping, int source, int destination, vector<State>& visited) {
        if (mapping[source].empty()) {
            if (source == destination) {
                return true;
            }
            return false;
        }
        if (visited[source] != notVisited) {
            return visited[source] == isTrue;
        }
        visited[source] = isFalse;
        for (const auto child : mapping[source]) {
            if (!dfs(mapping, child, destination, visited)) {
                return false;
            }
        }
        visited[source] = isTrue;
        return true;
    }
public:
    bool leadsToDestination(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<vector<int>> mapping(n, vector<int>());
        for (const auto& edge : edges) {
            mapping[edge[0]].push_back(edge[1]);
        }
        vector<State> visited(n, notVisited);
        return dfs(mapping, source, destination, visited);
    }
};

示例代码 (java)

class Solution {
    enum State { PROCESSING, PROCESSED }
    
    public boolean leadsToDestination(int n, int[][] edges, int src, int dest) {
        List<Integer>[] graph = buildDigraph(n, edges);
        return leadsToDest(graph, src, dest, new State[n]);
    }
    
    private boolean leadsToDest(List<Integer>[] graph, int node, int dest, State[] states) {
        if (states[node] != null) return states[node] == State.PROCESSED;
        if (graph[node].isEmpty()) return node == dest;
        states[node] = State.PROCESSING;
        for (int next : graph[node]) {
            if (!leadsToDest(graph, next, dest, states)) return false;
        }
        states[node] = State.PROCESSED;
        return true;
    }
    
    private List<Integer>[] buildDigraph(int n, int[][] edges) {
        List<Integer>[] graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            graph[edge[0]].add(edge[1]);
        }
        return graph;
    }
}

示例代码 (python)

class Solution:
    def leadsToDestination(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        def dfs(i):
            seen.add(i)
            for j in graph[i]:
                if j == i or j in seen or not dfs(j):
                    return False
            seen.discard(i)
            return len(graph[i]) != 0 or i == destination
        graph, seen = collections.defaultdict(set), set()
        for a, b in edges:
            graph[a].add(b)
        return dfs(source)

复杂度分析

时间复杂度: O(N)
空间复杂度: O(N)

归纳总结

我们在Youtube上更新了视频讲解，欢迎关注！