[Leetcode 1036] Escape a Large Maze

Posted on | In | Comments: | Views:

原题说明

In a 1 million by 1 million grid, the coordinates of each grid square are (x, y) with 0 <= x, y < 10^6.

We start at the source square and want to reach the target square. Each move, we can walk to a 4-directionally adjacent square in the grid that isn’t in the given list of blocked squares.

Return true if and only if it is possible to reach the target square through a sequence of moves.

Example 1:

Input: blocked = [[0,1],[1,0]], source = [0,0], target = [0,2]
Output: false
Explanation: The target square is inaccessible starting from the source square, because we can’t walk outside the grid.

Example 2:

Input: blocked = [], source = [0,0], target = [999999,999999]
Output: true
Explanation: Because there are no blocked cells, it’s possible to reach the target square.

Note:

  1. 0 <= blocked.length <= 200
  2. blocked[i].length == 2
  3. 0 <= blocked[i][j] < 10^6
  4. source.length == target.length == 2
  5. 0 <= source[i][j], target[i][j] < 10^6
  6. source != target

解题思路

题目给我们一个1百万乘1百万的迷宫，同时告诉你其中一些点是阻隔的，不能通过。问你是否有一条通路可以从点source连接到target。

按照常规思路，我们首先想到的肯定是用DFS或者BFS的方法，从一个点开始，暴力搜索所有能到的点。但是，由于迷宫非常大，这样做的时间复杂度会达到O(10^12)，你提交的解法会 TLE。

我们回头仔细看题目给我们的Note, 发现blocked的长度是有限制的，最多不超过200。这能给我们带来启发。首先，两个点之所以不能联通，一定是因为被blocked中的点分隔开了。那意味着blocked中的点能将迷宫分割成两个部分，每个部分分别包含source和target中的一个点。而因为blocked的点数量不超过200，因此，它所能围城的面积也是有限制的。

我们可以将问题抽象成这样一个数学问题，在一个1000000 \* 1000000的矩形中，用一条长200的线，最多能围出多大的面积？这个问题可以用泛函的知识求解，这里不多做说明。但其实我们利用对称性可以知道，在任意一个角，围出一个弧长200的1/4圆就是最大的面积，也就是4/pi \* 10000。

知道了这个面积，我们只需要对source和target分别做两次BFS。每次BFS，我们设定所搜的次数不超过我们求出的这个最大面积。如果在这些点中找到了target或source,那自然说明有这样一条通路。否则：

  1. 如果我们发现BFS在我们设定的搜索次数内，已经完成，那么说明source或者target处于被blocked点和迷宫边界构成的一个封闭区间内，不存在通路。
  2. 如果BFS在设定的搜索次数内没有完成，说明并没有这样一个封闭区间能包裹住source或者target,那它们两个点一定是能够连通的。

下图给出target和source别阻隔时，可能的情况。(图片引子Discuss中2017111303的帖子)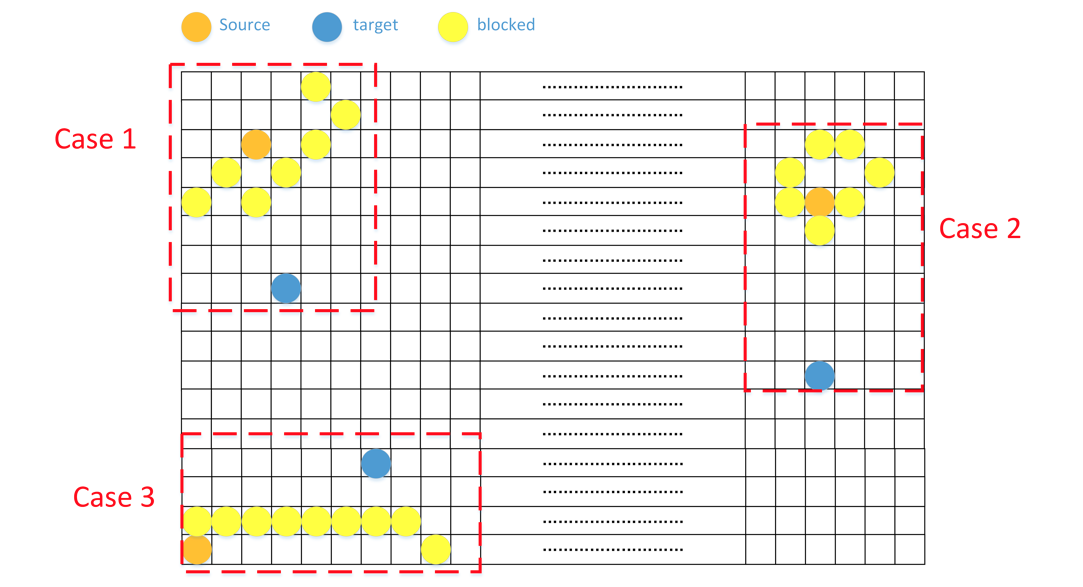

示例代码 (cpp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
private:
    unordered_set<long long> bSet;
    const long long  len = 1000000;
    const int maxArea = 4/3.14*10000;
public:
    bool isEscapePossible(vector<vector<int>>& blocked, vector<int>& source, vector<int>& target) {
        for (auto b : blocked) {
            bSet.insert(static_cast<long long>(b[0] * len + b[1]));
        }
        return bfs(source, target) && bfs(target, source);
    }
    bool bfs(vector<int>& source, vector<int>& target) {
        deque<vector<int>> q;
        unordered_set<long long> aSet;
        vector<vector<int>> dirs = {{1,0},{-1,0},{0,1},{0,-1}};
        q.push_back({source[0], source[1]});
        
        while (q.size() != 0 && aSet.size() < maxArea) {
            int r = q.front()[0];
            int c = q.front()[1];
            if (r == target[0] && c == target[1]) {
                return true;
            }
            aSet.insert(r * len + c);
            for (auto dir : dirs) {
                int rNew = r + dir[0];
                int cNew = c + dir[1];
                if (rNew >= 0 && rNew < len && cNew >= 0 && cNew < len) {
                    long long locNew = rNew * len + cNew;
                    if (aSet.find(locNew) == aSet.end() && bSet.find(locNew) == bSet.end()) {
                        q.push_back({rNew, cNew});
                        aSet.insert(locNew);
                    }                    
                }
            }
            q.pop_front();
        }
        return aSet.size() >= maxArea;
    }
};

示例代码 (java)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    Long M = 1000000L;
    int[][] dirs = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};
    
    public boolean isEscapePossible(int[][] bs, int[] s, int[] t) {
        Set<Long> b = new HashSet<>();
        for(int[] n : bs) b.add(n[0]*M + n[1]);
        return check(b, s, t, s, new HashSet<>()) && check(b, t, s, t, new HashSet<>());//make sure that both s ant t will not be surrouded by the block.
    }
    
    
    boolean check(Set<Long> b, int[] s, int[] t, int[] p, Set<Long> v) {
        if(Math.abs(p[0] - s[0]) == 200 || Math.abs(p[1] - s[1]) == 200 || v.size() > 0 && p[0] == t[0] && p[1] == t[1]) return true;
        
        v.add(p[0]*M+p[1]);
        for(int[] dir : dirs) {
            int x = p[0] + dir[0], y = p[1] + dir[1];
            if(x < 0 || x == M || y < 0 || y == M || v.contains(x*M+y) || b.contains(x*M+y)) continue;
            if(check(b, s, t, new int[]{x, y}, v)) return true;
        }
        return false;
    }
}

示例代码 (python)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution(object):
    def isEscapePossible(self, blocked, source, target):
        """
        :type blocked: List[List[int]]
        :type source: List[int]
        :type target: List[int]
        :rtype: bool
        """
        if not blocked: return True
        blocked = set(map(tuple, blocked))
        
        def check(blocked, source, target):
            si, sj = source
            ti, tj = target
            level = 0
            q = collections.deque([(si,sj)])
            vis = set()
            while q:
                for _ in range(len(q)):
                    i,j = q.popleft()
                    if i == ti and j == tj: return True
                    for x,y in ((i+1,j),(i-1,j),(i,j+1),(i,j-1)):
                        if 0<=x<10**6 and 0<=y<10**6 and (x,y) not in vis and (x,y) not in blocked:
                            vis.add((x,y))
                            q.append((x,y))
                level += 1
                if level == len(blocked): break
            else:
                return False
            return True
        
        return check(blocked, source, target) and check(blocked, target, source)

复杂度分析

时间复杂度: O(len(blocked)^2)
空间复杂度: O(len(blocked))

归纳总结

我们在Youtube上更新了视频讲解，欢迎关注！

Related Posts
------ 关注公众号：猩猩的乐园 ------