[Leetcode 1028] Recover a Tree From Preorder Traversal

原题说明

We run a preorder depth first search on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. (If the depth of a node is D, the depth of its immediate child is D+1. The depth of the root node is 0.)

If a node has only one child, that child is guaranteed to be the left child.

Given the output S of this traversal, recover the tree and return its root.

Example 1: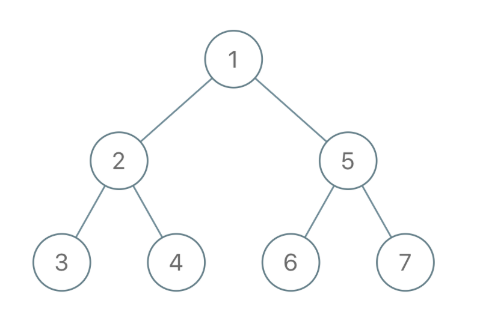

Input: "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

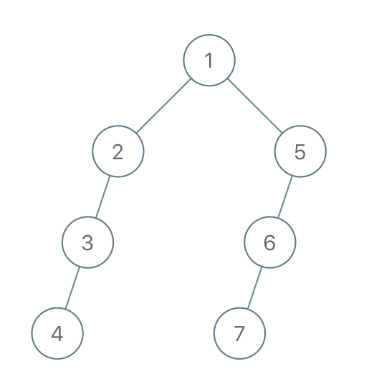
Input: "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

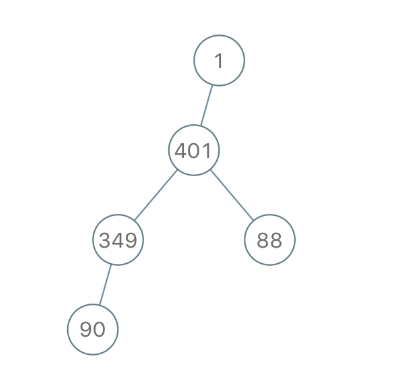
Input: "1-401--349---90--88"
Output: [1,401,null,349,88,90]

解题思路

parse String S, 遍历获取每个node以及它对应的level。类似于用非递归法前序遍历二叉树，我们来重构二叉树。使用stack的数据结构(这里我们用vector代替stack，本质是一样的）。stack的size就是当前遍历到的二叉树的深度。当stack.size() > level时，意味着当前节点为根节点的子树都被遍历过了，需要退栈，直到stack.size == level，插入当前新遍历到的node。

最后返回stack[0]， 即二叉树的根节点。

示例代码 (cpp)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* recoverFromPreorder(string S) {
        vector<TreeNode*> stack;
        for (int i = 0; i < S.size();) {
            int level;
            int val;
            for (level = 0; S[i] == '-'; i++) {
                level++;
            }
            for (val = 0; S[i] != '-' && i < S.size(); i++) {
                val = val * 10 + S[i] - '0';
            }
            while (stack.size() > level) {
                stack.pop_back();
            }
            TreeNode* node = new TreeNode(val);
            if (!stack.empty()) {
                if (stack.back()->left) {
                    stack.back()->right = node;
                }
                else {
                    stack.back()->left = node;
                }
            }
            stack.push_back(node);
        }
        return stack[0];
    }
};

示例代码 (java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode recoverFromPreorder(String S) {
        int level, val;
        Stack<TreeNode> stack = new Stack<>();
        for (int i = 0; i < S.length();) {
            for (level = 0; S.charAt(i) == '-'; i++) {
                level++;
            }
            for (val = 0; i < S.length() && S.charAt(i) != '-'; i++) {
                val = val * 10 + (S.charAt(i) - '0');
            }
            while (stack.size() > level) {
                stack.pop();
            }
            TreeNode node = new TreeNode(val);
            if (!stack.isEmpty()) {
                if (stack.peek().left == null) {
                    stack.peek().left = node;
                } else {
                    stack.peek().right = node;
                }
            }
            stack.add(node);
        }
        while (stack.size() > 1) {
            stack.pop();
        }
        return stack.pop();
    }
}

示例代码 (python)

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def recoverFromPreorder(self, S):
        """
        :type S: str
        :rtype: TreeNode
        """
        stack, i = [], 0
        while i < len(S):
            level, val = 0, ""
            while i < len(S) and S[i] == '-':
                level, i = level + 1, i + 1
            while i < len(S) and S[i] != '-':
                val, i = val + S[i], i + 1
            while len(stack) > level:
                stack.pop()
            node = TreeNode(val)
            if stack and stack[-1].left is None:
                stack[-1].left = node
            elif stack:
                stack[-1].right = node
            stack.append(node)
        return stack[0]

复杂度分析

时间复杂度: O(n)
空间复杂度: O(n)

归纳总结

我们在Youtube上更新了视频讲解，欢迎关注！