[Leetcode 1026] Maximum Difference Between Node and Ancestor

原题说明

Given the root of a binary tree, find the maximum value V for which there exists different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

(A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.)

Example 1: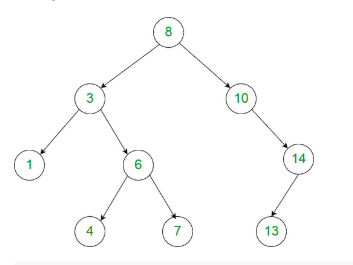

Input: [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation:
We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Note:

1. The number of nodes in the tree is between 2 and 5000.
2. Each node will have value between 0 and 100000.

解题思路

这道题有两种解法，自下而上记录下子树的最大与最小值，或者自上而下记录下子树的最大与最小值。需要注意的事，自下而上的方法需要后序遍历二叉树，自上而下则需要前序遍历二叉树。

这里我们采用自上而下的方法前序遍历二叉树。每次更新从根节点到当前节点的路径中，最大值与最小值的差的绝对值。因为是在一条路径中，所以其中一个节点一定是另外一个节点的祖先。又因为是前序遍历二叉树，时间复杂度就是O(n)。

示例代码 (cpp)

class Solution {
public:
    int maxAncestorDiff(TreeNode* root) {
        return maxAncestorDiffHelper(root);
    }
    int maxAncestorDiffHelper(TreeNode* root, int imax = INT_MIN, int imin = INT_MAX) {
        if(root == nullptr)
            return 0;        
        //root
        imax = max(imax, root -> val);
        imin = min(imin, root -> val);
        v_max = max(v_max, abs(imax - imin));
        maxAncestorDiffHelper(root -> left, imax, imin);//go to left child
        maxAncestorDiffHelper(root -> right, imax, imin);//go to right child
        
        return v_max;  
    }    
private:
    int v_max = 0;
};

示例代码 (python)

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def __init__(self):
        self.v_max = 0
    def maxAncestorDiff(self, root, imax = 0, imin = 5001):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root == None:
            return 0
        imax = max(imax, root.val)
        imin = min(imin, root.val)
        self.v_max = max(self.v_max, abs(imax - imin))
        self.maxAncestorDiff(root.left, imax, imin)
        self.maxAncestorDiff(root.right, imax, imin)
        return self.v_max

复杂度分析

时间复杂度: O(n)
空间复杂度: O(1)

归纳总结

我们在Youtube上更新了视频讲解，欢迎关注！